林宥呈
6 November 2025
討論區
假設 $V$ 為 vector space 且 $W$ 為其 subspace。考慮 $S=(V\backslash W)\cup\{\mathbf{0}\}$。
(Note:$V\backslash W=\{\mathbf{v}\in V|\mathbf{v}\notin W\}$)
(a) 說明當 $W=V$ 或 $W=\{\mathbf{0}\}$ 時,$S$ 會是 $V$ 的 subspace。
(b) 證明當 $W\neq V$ 且 $W\neq\{\mathbf{0}\}$(即 $W$ 為 $V$ 的 nontrivial subspace)時,$S$ 一定不會是 $V$ 的 subspace。
幾個建議
- 解法若無太大差異,請不要重複。
- 符號的使用請注意。這裡因為有 $V$ 還有聯集 $\bigcup$,"或"、"且" 應避免用 $\vee$, $\wedge$。
- 論述過於冗長,避免不必要敘述且適時說明到哪些條件。例如 (b) 不需一開始列出所有條件。只要提到因 $W\ne V$ 所以 $V\setminus W\ne \emptyset$ 即可。最後清楚寫下找到哪兩個元素不符合加法封閉。
題目問的是 $S$,但整個論述沒有 $S$ 不會很奇怪嗎?例如(a)寫:當 $W=V$ 時,$S=\left(V\setminus V\right)\cup\{\mathbf{0}\} = \emptyset\cup\{\mathbf{0}\}=\{\mathbf{0}\}$。是不是比較清楚?
這個問題是針對許多同學誤以為 vector space 扣掉 subspace 再補上零向量還是 vector space。論證時會發現滿足係數積封閉性(請務必自行論證);但不滿足加法封閉。是不是和我們談 subspace 的聯集很像呢?希望大家能善用課堂上所學(這樣才有學到新的東西)。其實此題本意是希望能用反證法,然後直接套用所學到有關 subspace 聯集的性質,就可得到矛盾。
本主題請 晴月夢 將所寫修改得更簡明,可得 2pts. ;其他同學若能完整補上前述反證法的論證(記住一定要說清楚何時用到前提假設),也可得 2pts.


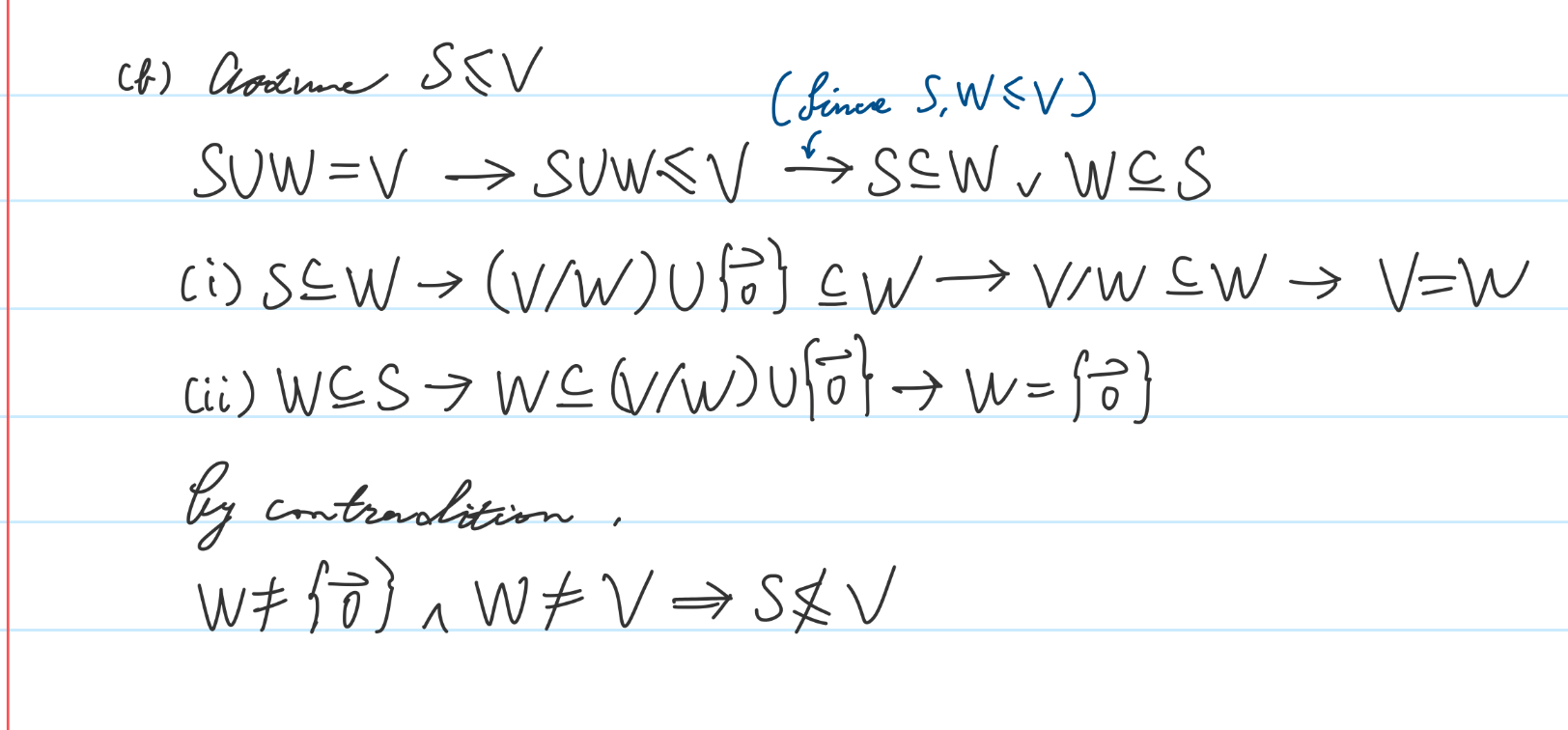
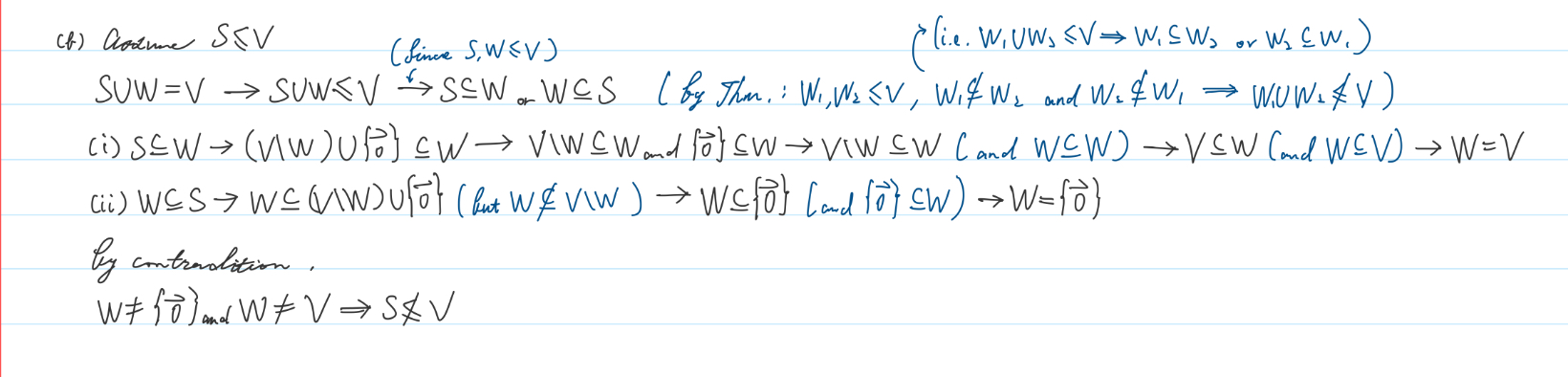


手寫證明過程,附部分解釋。
手寫證明過程
我附上了兩個版本,為了收穫證明撰寫的反饋,以準備段考。
建議直接從第二版開始看。
證明過程中,我們省略了:
我不確定這樣在段考中合不合法。
第一版:
第二版:
解釋
(a) 小題利用到 $V$ 的 trivial subspaces ——$\{\mathbf{0}\}$ 和 $V$。分情況,化簡過後即可自然發現。
(b) 小題過程用 constructive(嗎?) 的辦法說明了為什麼 $S$ 通常不會是 $V$ 的 subspace —— 加法沒有封閉性。藉此,足以回答題目。
我們從 $V\setminus W$ 和 $W\setminus \{\mathbf{0}\}$ 中找向量,最後構成一個反例。
也就是說,如果 $W = \{\mathbf{0}\}$ 或 $W = V$,$V\setminus W$ 和 $W\setminus \{\mathbf{0}\}$ 有一個是空集合,(b) 小題的方法就不會成立了。這也揭示了找到證明思路的方法。
$\mathbf{0}$ 顯然在 $S$ 裡。那麼,我們尚未說明的是, $S$ 裡的向量的係數積,有封閉性嗎?
請多指點。
PS:又到了煩惱如何撰寫易讀達意嚴謹證明的時節了。