討論區
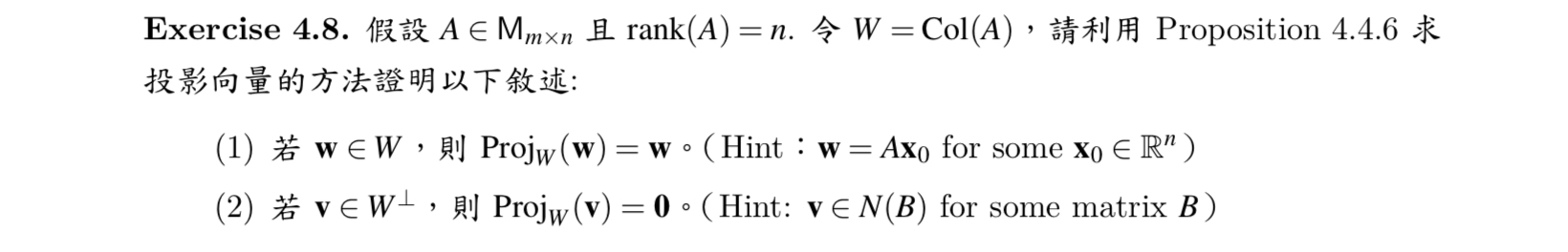
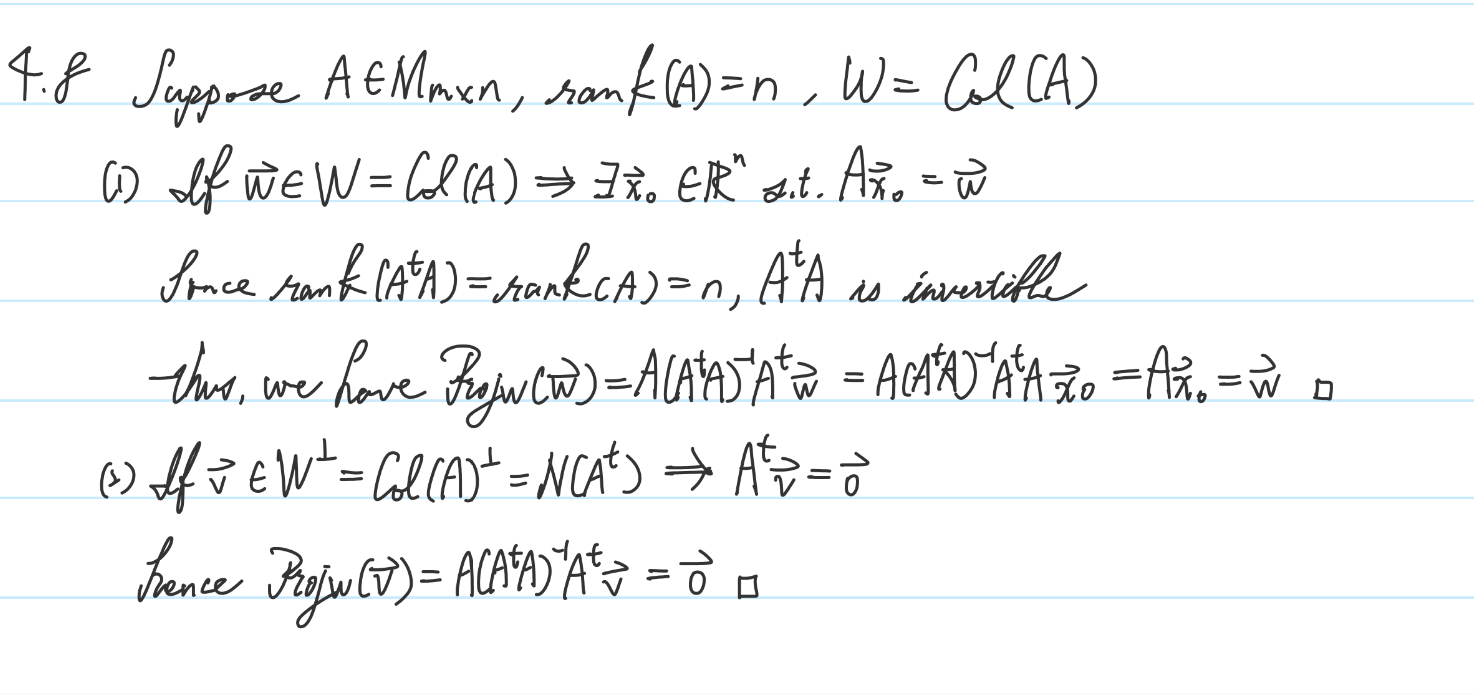
存在不要亂用
tsai0314 對於 Proposition 4.4.6 從新敘述有問題(存在不要亂用)。
(1) 的論證不錯(此處存在的用法很正確),也確實掌握 Proposition 4.4.6 的重點,即:「只要 $\mathbf{x}_0$ 為方程組 $(A^tA)\mathbf{x}=A^t\mathbf{v}$ 的一解,則 $A\mathbf{x}_0$ 就是 $\mathbf{v}$ 在 $W$ 的投影。
不過(2)的論述,又讓人懷疑到底 tsai0314 了解 Proposition 4.4.6 嗎?方程組是什麼?解是什麼?(存在又亂用了!明明有具體的解)。看看有誰能給(2)一個簡明的論述。
請 tsai0314 用自己了解的方式重新敘述 Proposition 4.4.6
我幫 tsai0314 重寫 (1) 的論述,大家想想 (2) 需要用到 $N(A^tA)=N(A)$ 這麼大的牛刀來殺雞嗎?
(1) 因 $\mathbf{w}\in W=\mathrm{Col}(A)$,故存在 $\mathbf{u}\in\mathbb{R}^n$ 滿足 $A\mathbf{u}=\mathbf{w}$。現考慮聯立方程組 $(A^tA)\mathbf{x}=A^t\mathbf{w}$。由 $(A^tA)\mathbf{u}=A^t(A\mathbf{u})=A^t\mathbf{w}$,知 $\mathbf{x}=\mathbf{u}$ 為聯立方程組 $(A^tA)\mathbf{x}=A^t\mathbf{w}$ 的一解。故由 Proposition 4.4.6 知 $\mathrm{Proj}_W(\mathbf{w})=A^t\mathbf{u}=\mathbf{w}$。
本主題結束
請大家注意,論壇寫的東西是給大家看的。越能表達清楚,讓其他不懂的同學能懂最重要。Proposition 4.4.6 就是後面 normal equation 的概念。它幫助我們簡化求投影的程序。基本上找到 normal equation 並求出一解,就可得求得投影向量。所以儘量寫清楚 normal equation 是什麼,讓人清楚如何得到一解。(3)就是說當 $\mathbf{v}\in W^\perp$,所要處理的 normal equation $(A^tA)\mathbf{x}=A^t\mathbf{v}$ 可具體表成方程組 $(A^tA)\mathbf{x}=\mathbf{0}$,所以可以明確的知道 $\mathbf{x}=\mathbf{0}$ 為其一解。因而求出 $\mathrm{Proj}_W(\mathbf{v})=A\mathbf{0}=\mathbf{0}$。


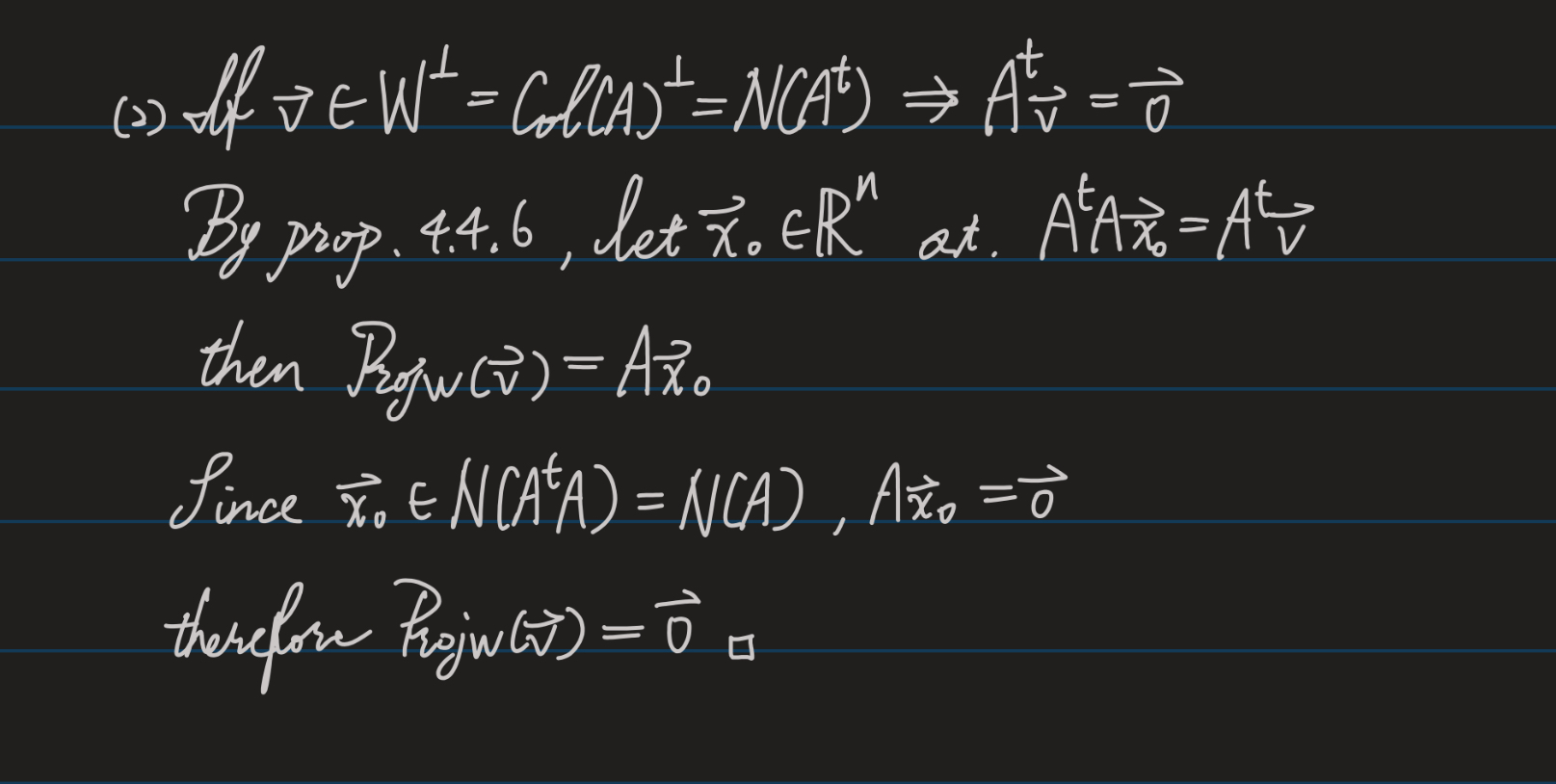

更正題目、請勿答非所問
Proposition 4.4.6 說什麼?另題目更正:不需 $\mathrm{rank}(A)=n$ 的假設