討論區

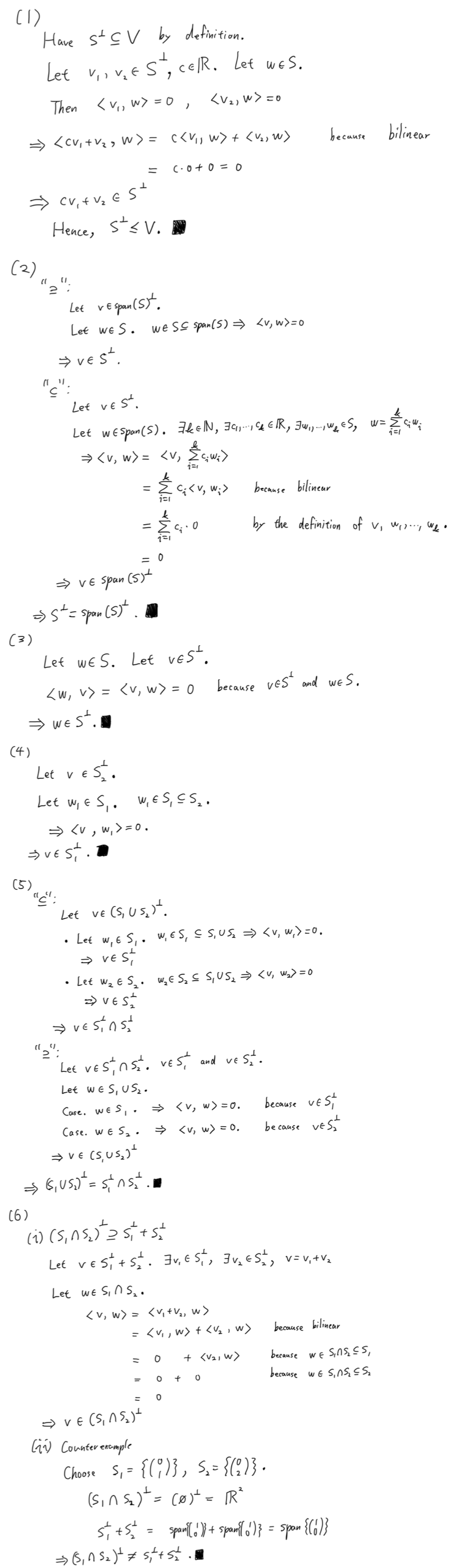
請善用(4)
首先注意:集合包含關係和說明在 $S^\perp$ 是有層次的,請避免都用 let,會讓人不懂哪個是固定的,最後又是要論證哪個包含關係。
例如(2) $\mathrm{Span}(S)^\perp\subseteq S^\perp$ 建議一開始是 given $\mathbf{v}\in \mathrm{Span}(S)^\perp$,接著是 $\forall\,\mathbf{w}\in S$ 讓人了解是給定 $\mathbf{v}$ 然後 $\mathbf{w}$ 是變動的,這樣最後這給定的 $\mathbf{v}$ (和最開始是同一個 $\mathbf{v}$) 會在 $ S^\perp$,才能確認包含關係。
前面的例子若先證明了(4)就能省掉一些論述。(5)(6)也可省掉部分用元素證明包含關係的論述,看看誰能補上。
補上使用 (4) 能省掉的論述
首先,(2) “$\supseteq$” 可以直接用 (4) 和 span 的定義 (?) 解決:
Start with \[S\subseteq \text{span}(S)\]
Then by (4), we can get the following conclusion directly: \[\text{span}(S)^{\perp}\subseteq S^{\perp}. \blacksquare\]
同時,(5) “$\subseteq$” 也可以用 (4) 和集合運算的性質解決:
Start with \[\begin{aligned}&S_1\subseteq S_1\cup S_2\\&S_2\subseteq S_1\cup S_2\end{aligned}\]
Then by (4), \[\begin{aligned}&(S_1\cup S_2)^{\perp}\subseteq S_1^{\perp}\\&(S_1\cup S_2)^{\perp}\subseteq S_2^{\perp}\end{aligned}\]
and therefore \[(S_1\cup S_2)^{\perp} \subseteq S_1^{\perp} \cap S_2^{\perp}.\blacksquare\]
最後是 (6) 的 $\subseteq$ 的部分:
Start with \[\begin{aligned}&S_1\cap S_2\subseteq S_1\\&S_1\cap S_2\subseteq S_2\end{aligned}\]
Then by (4), \[\begin{aligned}&S_1^{\perp}\subseteq(S_1\cap S_2)^{\perp}\\&S_2^{\perp}\subseteq(S_1\cup S_2)^{\perp}\end{aligned}\]
Therefore, since $S_1^{\perp}$ and $S_2^{\perp}$ are subspaces of V by (1), and $S_1^{\perp} + S_2^{\perp}$ is the smallest subspace that contains them, we have \[S_1^{\perp} + S_2^{\perp} \subseteq (S_1\cap S_2)^{\perp}.\blacksquare\]
關於先前表達上的問題,有時間我再補上優化版本。感謝指導。




(1) subspace要記得證明非空(3)…
(1) subspace要記得證明非空
(3) 你完全沒說到題目要求的內容,而且 $\mathbf{w}\in W$ 後為何又推出 $\mathbf{w}\in W^{\perp}$??
然後目前你的證明會讓人有點看不太懂你想表達什麼,有些過程跳的太突然了,給你一些小方法會讓證明比較好看