討論區

請大家想辦法好好寫好這一題
前面已提過,本題的重點是將一般向量空間($\mathbb{R}^n$ 以外的 vector space),可以像 $\mathbb{R}^n$ 一樣,利用矩陣(而不是解聯立方程)來判定向量之間的線性關係。這對以後處理一般向量空間的問題很重要,希望大家集思廣益寫下很好的論述,讓它像定理一樣,以後可以好好使用。若對他人寫的有覺得任何不完善之處,請具體寫出較完善的論述。只有老師或助教使用提示方式建議修改方向,其餘同學請具體寫下覺得較完善的論述,不要用提示方式;否則他人無法判定想法是否正確。
(1)的用意是希望將 $x_1\mathbf{w}_1+x_2\mathbf{w}_2+x_3\mathbf{w}_3=\mathbf{0}$ 的解集合和方程組 $A\mathbf{x}=\mathbf{0}$ 的解集合連結。希望同學能說明它們是一樣的且在證明它們之間包含關係時註明哪一個包含關係需要用到 $\mathbf{v}_1,\mathbf{v}_2, \mathbf{v}_3$ 為 linearly independent。
(2)希望用到(1)所得的解集合相等關係,直接套用我們了解有關利用矩陣 $A$ 來判定 $A\mathbf{x}=\mathbf{0}$ 的解集合的方法,得到 $\mathbf{w}_1,\mathbf{w}_2, \mathbf{w}_3$ 為 linearly independent 和矩陣 $A$ 的某特性的等價關係。證明等價時也請註明哪個論證方向需用到 $\mathbf{v}_1,\mathbf{v}_2, \mathbf{v}_3$ 為 linearly independent。
(3)希望大家能推廣(2)到更一般的狀況。請先寫下如(2)的結論,即 $\mathbf{w}_1,\dots, \mathbf{w}_m$ 為 linearly independent 若且唯若 "矩陣 $A$ 的某特性",並證明之。
糬 (1)就沒探討兩個解集合的關係(2)一開頭寫的若則問題就很大(邏輯敘述用法完全不正確)(3)不是 $\mathbb{R}^n$,哪來的矩陣 $[\mathbf{w}_1,\dots,\mathbf{w}_m]$ 又整個論述為何牽扯到 $m,n$ 的大小關係呢?






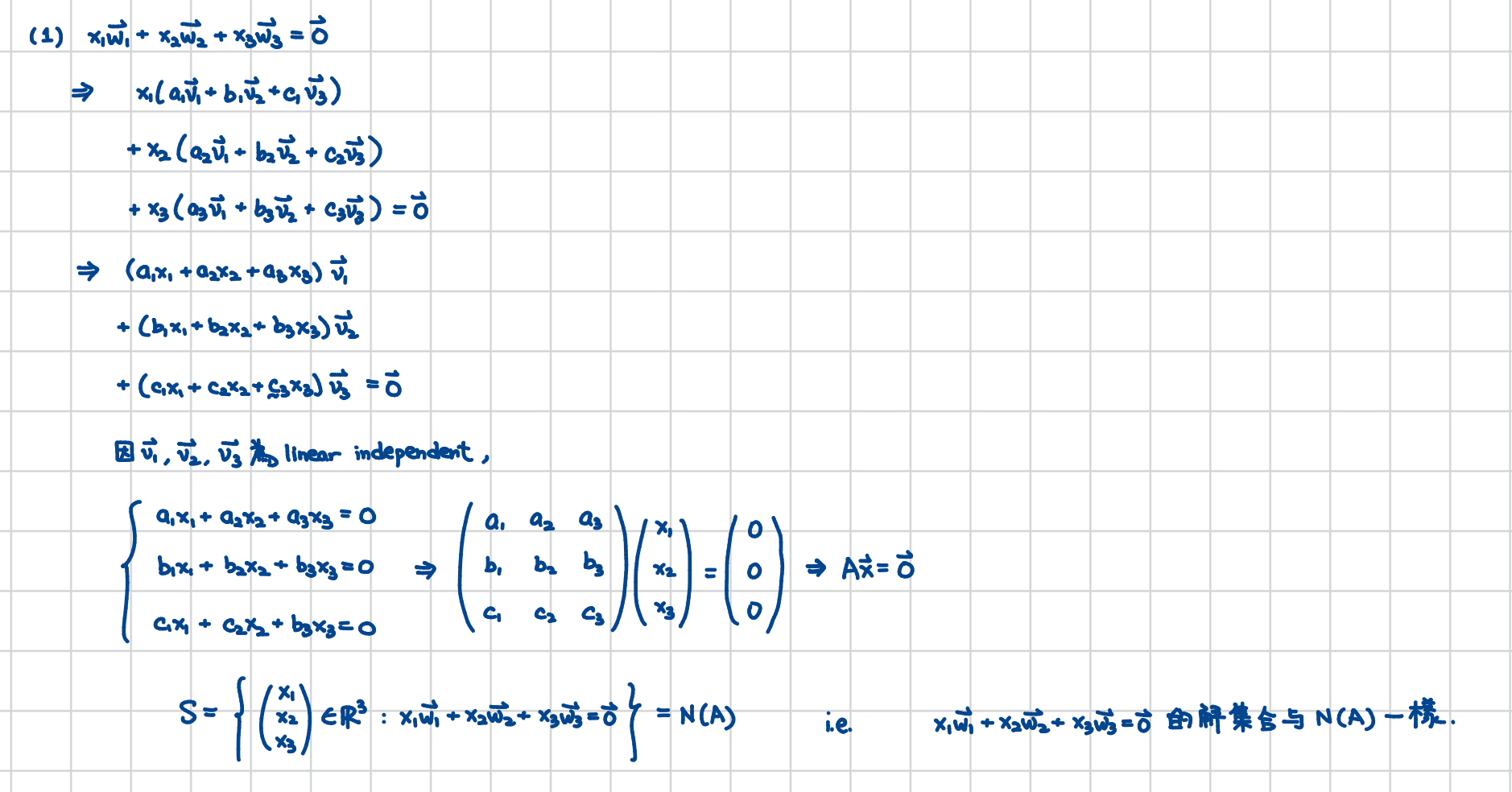
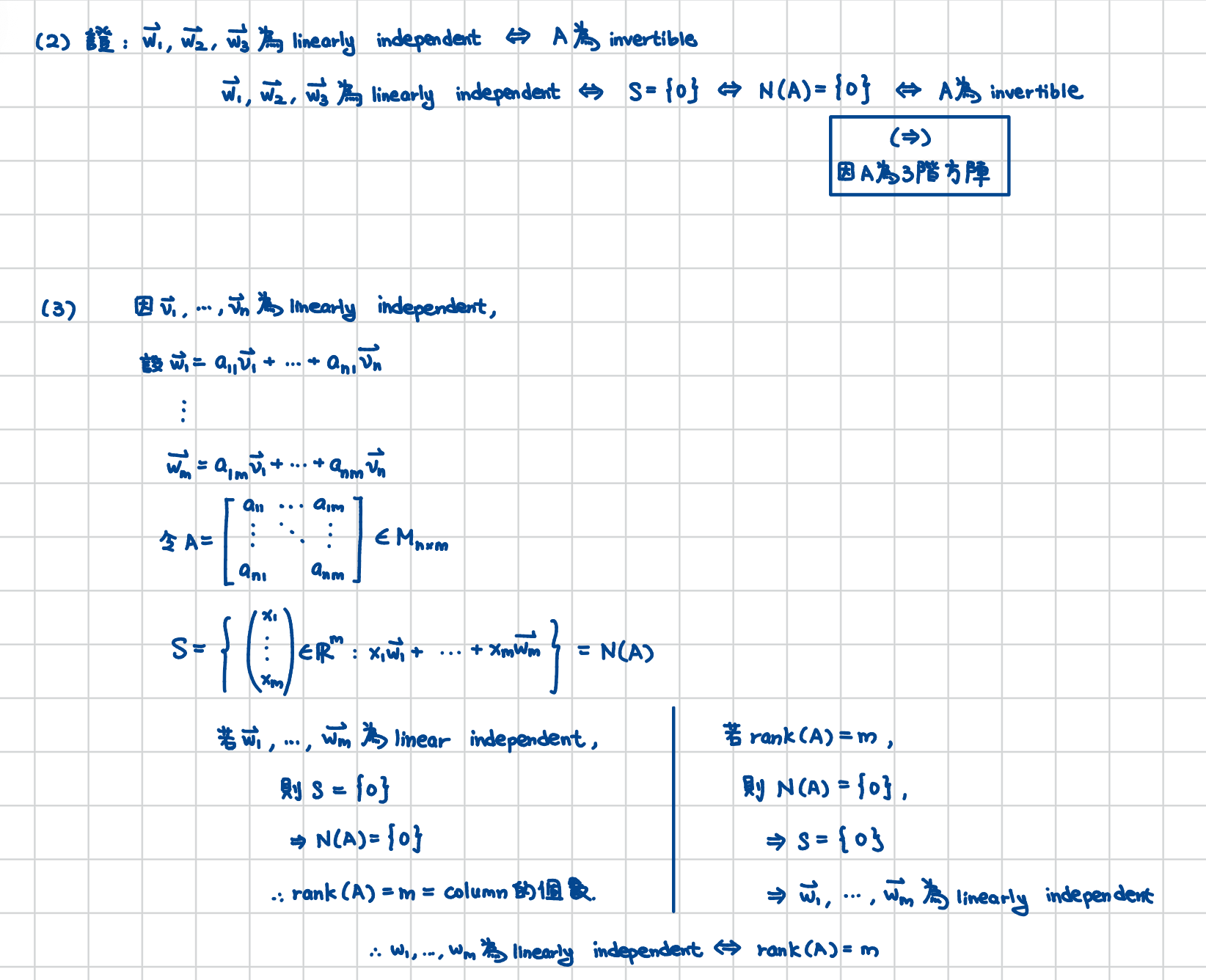
(3)沒有考慮到若m小於等於n,且係數矩陣A的rank(A…
(3)沒有考慮到若m小於等於n,且係數矩陣A的rank(A)小於m時的情況