討論區

幾個建議
一塊土 的想法很有創意。利用數學歸納法給出定義並用已論證過 $n=2$ 的情形在(ii)(a)輕鬆地證明了 $W_1+\cdots+W_{k+1}$ 是包含 $W_1,\dots,W_{k+1}$ 的 subspace。這裡建議補上由 $n=2$ 成立得知,另外此處不需用到"最小" (後面 (ii)(b)才要用到)可將此二字刪除。接著(ii)(b)要證明最小,就出問題了(與"聯集"搞混了)。請同學(或 一塊土 本人)幫忙揪錯。最後因為手寫"大小寫"要注意:元素和集合容易混淆。建議元素都用向量表示。
包子入侵 自行找出定義寫法錯誤之處,很好!封閉性的驗證,請避免沒有必要的足碼符號:$\mathbf{w}_{a_i}$ 容易讓人誤解有排列問題,可考慮用 $\mathbf{w}_i, \mathbf{w}'_i$ 即可。證明最小的部分,用集合方式的證明是無效的:直接說 $W_1\subseteq U,\cdots,W_n\subseteq U$ 得到 $W_1+\cdots+W_n\subseteq U$ 有何用?這就是原本希望證明的啊!我猜測 包子入侵 和 一塊土 一樣都把向量空間的 sum 和 union 搞混了。在集合的情況確實可由 $W_1\subseteq U,\cdots,W_n\subseteq U$ 得到 $W_1\cup\cdots\cup W_n\subseteq U$,但這和向量空間的 sum 是兩回事。請 包子入侵 將這個無效論證刪除。在此也請大家注意,此處"最小"我們僅能用元素來論證;但論證完了這"最小"的性質後,以後就可以不必用元素直接用集合(其實是子空間)處理有關於子空間的包含關係。
一塊土 數學歸納法論證的建議
這是較進階的數學歸納法論述:一個歸納假設同時證明 (a) $W_1+\cdots+W_n$ 是包含 $W_1,\dots,W_n$ 的 vector space 以及 (b) 是所有包含 $W_1,\dots,W_n$ 的 vector space 中最小的 vector space。要學好這種論述就要精準的了解其真義,而不是意思到了就好。希望 一塊土 針對我說的缺失,精準的寫下一個完美的論述。對於其他想好好學習數學歸納法論述的同學,若能清楚理解這個論述的真義,那很棒!若無法理解,也歡迎針對不清楚的地方提出討論。
為了讓同學清楚論述請 一塊土 在(i) $n=2$ 以及 (ii) $n=k$ 的歸納假設也分成(a),(b)敘述。改良的(ii)(a)目前寫得很清楚;但是(b)為何改成反證法呢?你已經將 $\mathbf{v}\in S_{k+1}$ 寫成 $\mathbf{v}=\mathbf{u}+\mathbf{w}_{k+1}$,然後證明了 $\mathbf{v}\in X$ 了!為何畫蛇添足,用反證法呢?
我們不只要學會對的事,也需要知道錯的是什麼!最後還是請同學(或是 一塊土)說明一下 一塊土 最原始的論述(ii)(b)錯在哪裡。
給 8879576 的建議
請注意 NOTATION !一看到一開始的符號使用,就令人滿頭霧水(我說過老師很笨都故意看不懂你們寫的東西; 一塊土 就看得懂真是令人佩服)。這裡的 $\alpha\in A$ 的 $A$ 是什麼?若 $A=\{1,\dots,n\}$ 所定義的 $W_1+\cdots+W_n=W_1\cap\cdots\cap W_n$ 不會很奇怪嗎?同樣的,出現了 $V_1$ 又定義 $V_n$ 也很奇怪?另外前面已提過手寫大小寫分不清,一下包含一下屬於,看的人若脾氣不好就把你退稿了!請記得看一下前面別人的帖子再回覆。
8879576 所用的概念是利用任意多個 subspace 交集仍為 subspace (Question 3.6, 包子入侵 有證明;可是寫得不夠完美,希望有人指正)來證明在一般的 vector space 中擁有某些特性的 subspace 一定有最小的。它很容易證明了存在性;但缺點是 non-constructive 的方式,因此這方法無法知道其元素。不過在我們的問題(即包含 $W_1,\dots,W_n$ 最小的 subspace),有 constructive 的方式,就是包子入侵 一開始的定義。所以 8879576 在此問題論證上的謬誤就是:沒有證明用交集所定義的就是所求;而是重寫一遍 包子入侵 已經論證的部分。正確的論證應是補上 Question 3.6 說明它是 subspace(順便將 包子入侵 的證明寫得更完美),再加上證明每個 $W_i$ 真的都在這個交集中(這是一般數學導論的習題)。證明完成後,就可以很帥的說 包子入侵 和 一塊土 用 constructive 的方式所得的 subspace 是最小的,而你定義的也是最小的。也就是說它們互相有包含關係,因此相等。








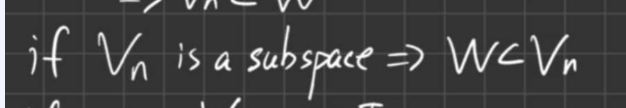
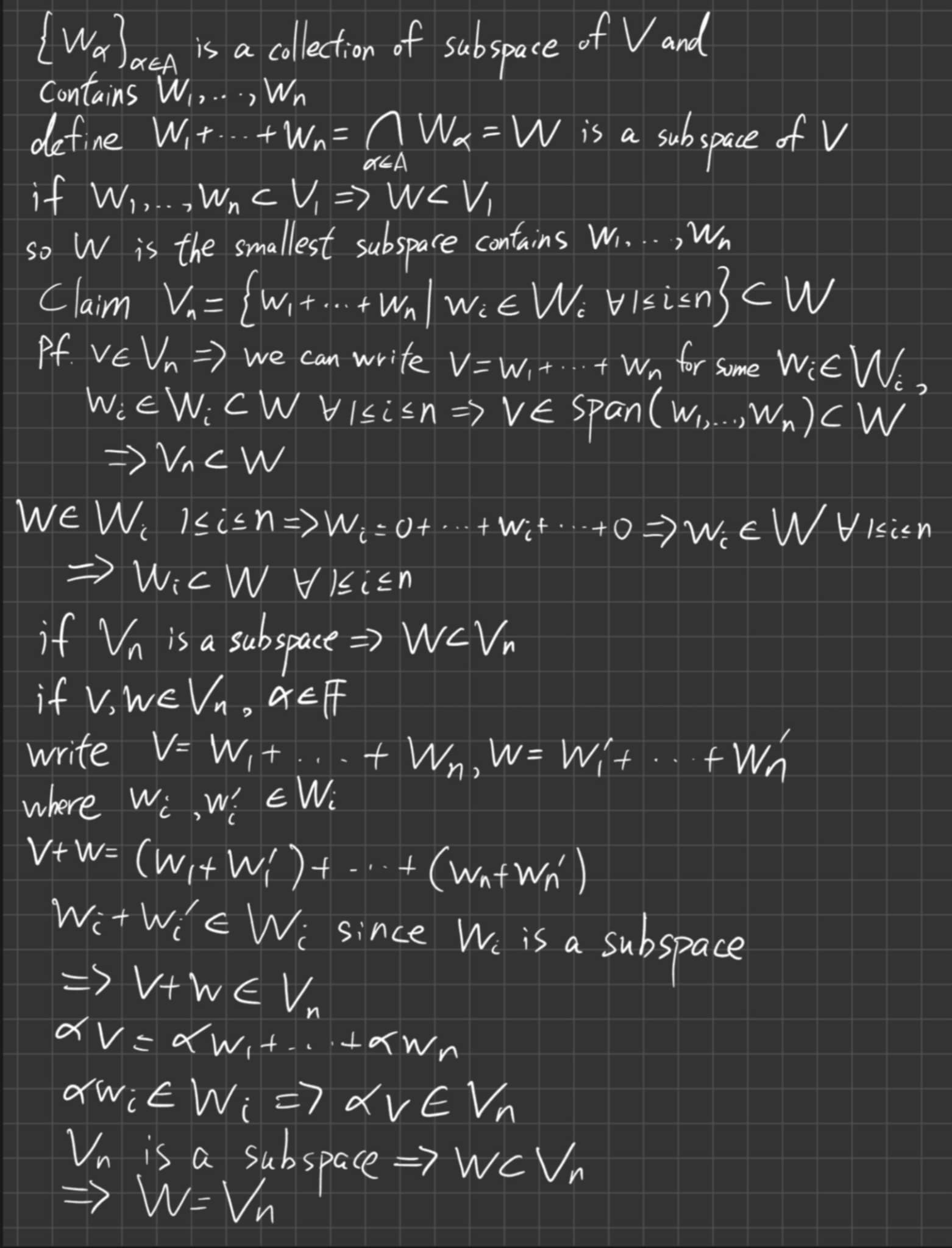

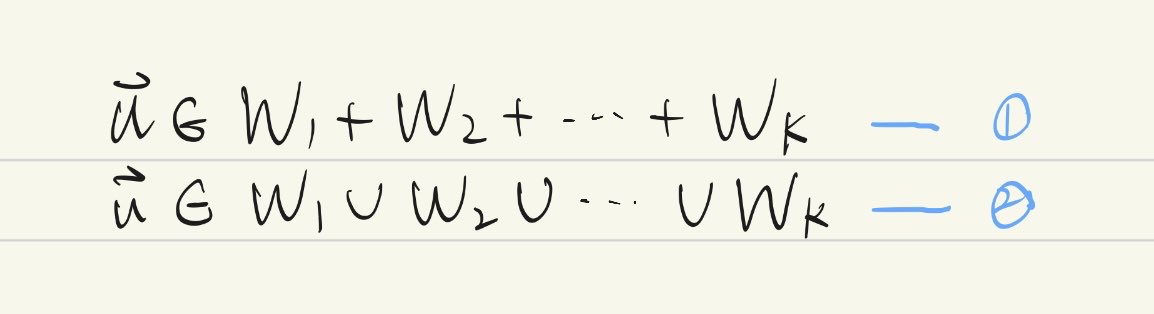


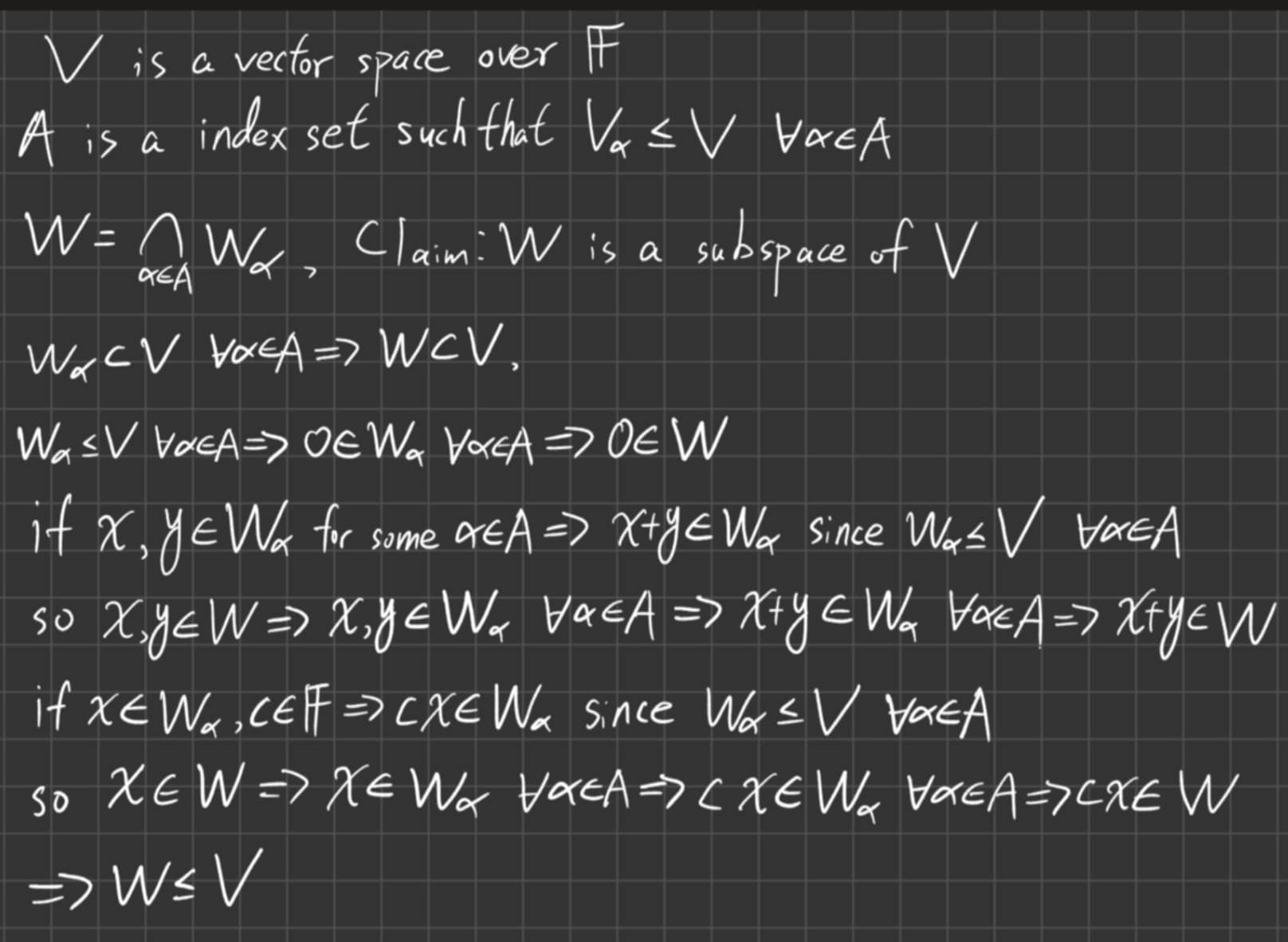
目前評論
包子入侵 $W_1+W_2+\cdots+W_n$ 定義有誤,是否有人能指正?最小的subspace 也完全沒有論證(注意:證明不是寫下"對的事")。
有誰能說好它?