討論區
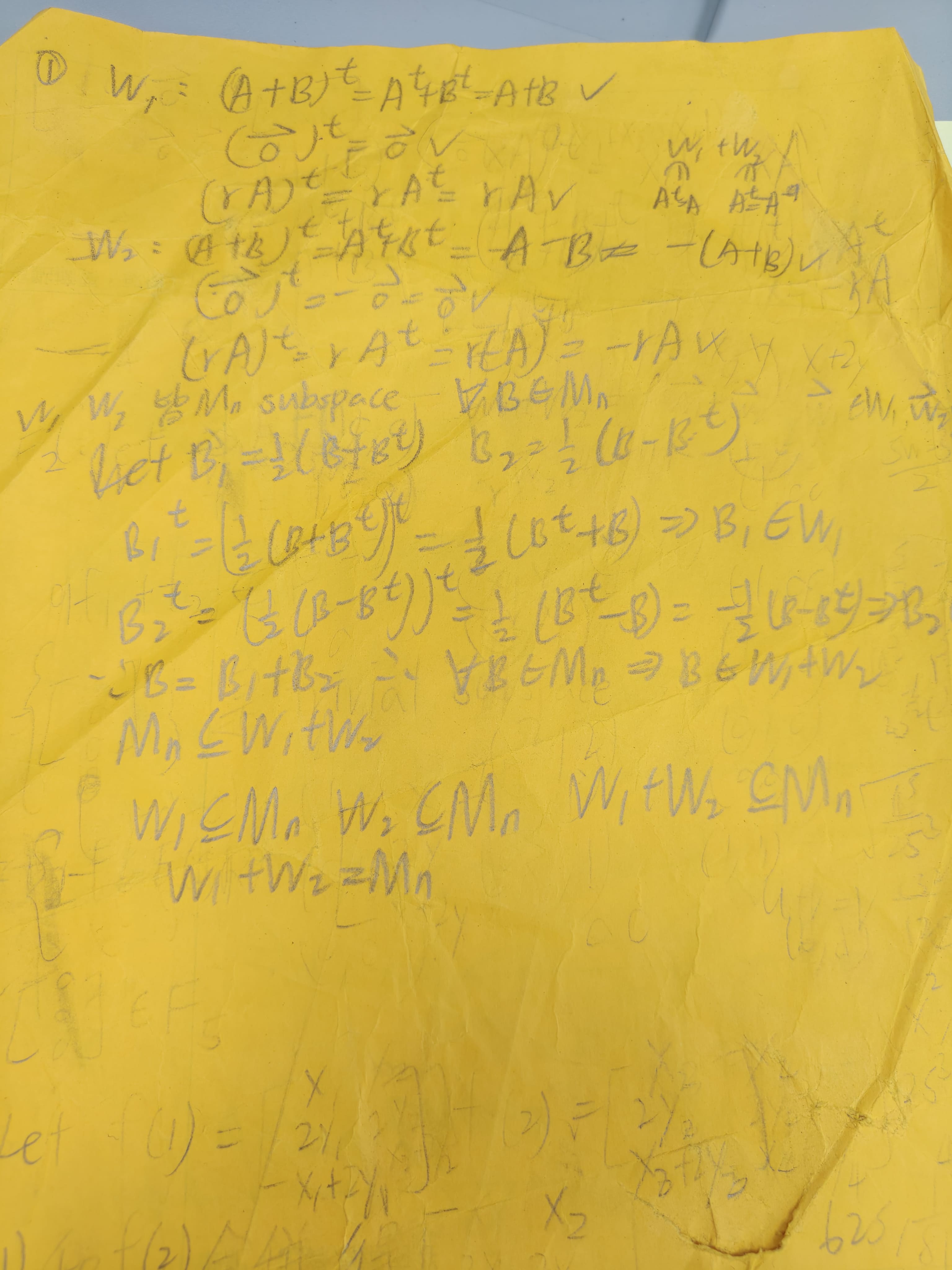
第 2 小題,有一般情況
說明
論證 \(W_3 ≤ M_n\) (也就是 \((I)\))的部分,我認為既然是從 entry 來看,把 notation 寫好會比較清楚。同時,舉出一個新的、特定的矩陣時,應該標注該矩陣為方陣,比如過程中 \(O_{n\times n}\in M_n\)。
論證 \(M_n \subseteq W_1 + W_3\) 的 (i) 部分,我們參考 包子入侵 的選法,根據所取的矩陣建構了兩個方陣來滿足要求,並在 (i)-1 部分中補足了必要敘述。
我當時在糾結要不要寫下該敘述的證明,最後認為其證明方式都是「分 case」、「拆定義」,而僅列出 (i)-2 的證明。
第 2 小題解法

本題結案
晴月夢 給了(2)清楚且詳細的解答。
包子入侵 其實一開始就理解如何處理一般情況,不過我們還是希望學生應該懂得如何用數學符號表達。雖然自己弄懂了!就能享受數學的快樂,但是畢竟還是要顧慮別人是否懂得你的想法。否則以後即使有了天大的發現,卻沒人能理解不就太可惜了?
張翔誠實名討論 再次的修正我終於看懂了。也因此才有辦法知道其想法有何缺失(所以還是希望大家能學會清楚表達想法)。大家應該不難發現晴月夢 、包子入侵 的論證都是從 $M_n$ 任取一個矩陣 $D$ 開始,然後想辦法找到 $W_1,W_3$ 中的矩陣 $B,C$ 使得 $D=B+C$,如此就完成了 $M_n\subseteq W_1+W_3$ 的論證。而 張翔誠實名討論 則是給了 $B\in W_1,C\in W_3$,然後想辦法說明 $B+C$ 會是什麼樣子。這樣的論述其實是證明 $W_1+W_3\subseteq M_n$ 這個原本成立的方向。雖然之中有解釋,但是邏輯上很難克服,這也是前面提到突然跑出個 $k$ 但不知何物的困境。所以請掌握『集合包含關係的論證方向』以及『存在性是要用已知的東西表達』,這兩個重要概念。也就是說 張翔誠實名討論 的論述中是要將 $b_{ij}$, $c_{ij}$ 用 $d_{ij}$ 來表示;而不是用 $b_{ij}$, $c_{ij}$ 來表示 $d_{ij}$。希望大家能理解其中差異。








第二小題