討論區
在此題的解法中,我們不特別列出使用到的 \(\mathbb{R}^3\) 的運算的性質。
(1)
令 \(h\) 為 \(F(S, \mathbb{R}^3)\) 的 zero vector。據其性質,知道對任意 \(f\in F(S, \mathbb{R}^3)\),\(f + h = f\) i.e. 根據定義,\[\begin{aligned}&(f + h)(1) = f(1) + h(1) = f(1) \Rightarrow h(1) = (0,0,0)\\&(f + h)(2) = f(2) + h(2)= f(2) \Rightarrow h(2) = (0,0,0).\blacksquare\end{aligned}\]
因為 \(S\) 只有 \(2\) 個元素,(1) 小題實際上已經完整的決定了函數 \(h\)。因為 \(F(S, \mathbb{R}^3)\) 是 vector space,保證 zero vector 的存在性,我們可以以此作結:\(F(S, \mathbb{R}^3)\) 的 zero vector 為 \(h\),以 \(h(1)=(0,0,0)\)、\(h(2)=(0,0,0)\) 定義。
接下來的過程中,我們將使用 \(h\) 來表示 \(F(S, \mathbb{R}^3)\) 的 zero vector。
(2)
\(h_1, h_2\in F(S, \mathbb{R}^3)\)
我們想依定義檢查 \((-2)h_1 + 2h_1 = h \)。如果該等式成立,\((-2)h_1\) 就是 \(2h_1\) 的 additive inverse,則依據 vector space 中任意元素的 additive inverse 的唯一性,就可以知道 \((-2)h_1 = -(2h_1)\)。
令 \(x\in S\)。\(x=1\lor x=2\)。\[\begin{aligned}((-2h_1)+2h_1)(x) &= (-2)(h_1(x))+2(h_1(x)) &\because\text{by definition}\\&=(0,0,0)&\because h_1(x)\in\mathbb{R}^3\\&=h(x)&\because\text{by the definition of }h\end{aligned}\]
因此,根據函數的定義,\((-2)h_1 + 2h_1 = h \)。$\blacksquare$
(3)
由 (2) 小題,我們知道 \(3h_2-2h_1 = 3h_2+(-(2h_1))=3h_2+(-2)h_1\)。則 \[\begin{aligned}(3h_2-2h_1)(1)&=(3h_2+(-2)h_1)(1)&\\&=3h_2(1)+(-2)h_1(1)&\because\text{by definition}\\&= 3(0,1,2)+(-2)(-1,2,-1)&\because\text{by the definition of }h_1, h_2\\&=(2, -1, 8)\end{aligned}\]\[\begin{aligned}(3h_2-2h_1)(2)&=(3h_2+(-2)h_1)(2)&\\&=3h_2(2)+(-2)h_1(2)&\because\text{by definition}\\&= 3(1,2,3)+(-2)(2,0,1)&\because\text{by the definition of }h_1, h_2\\&=(-1, 6, 7).\blacksquare\end{aligned}\]
第 \(4\) 小題留著,給大家接力完成。



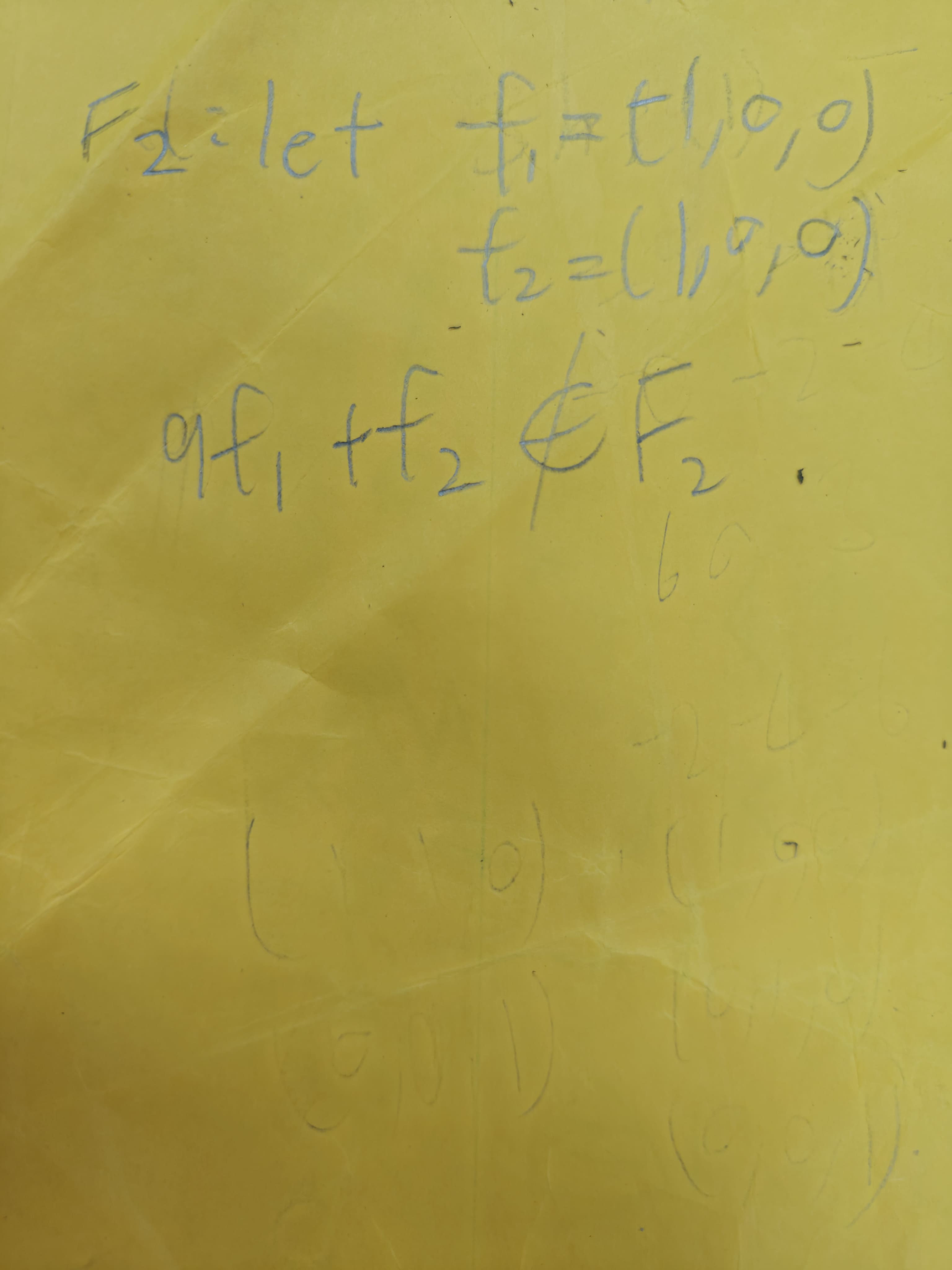


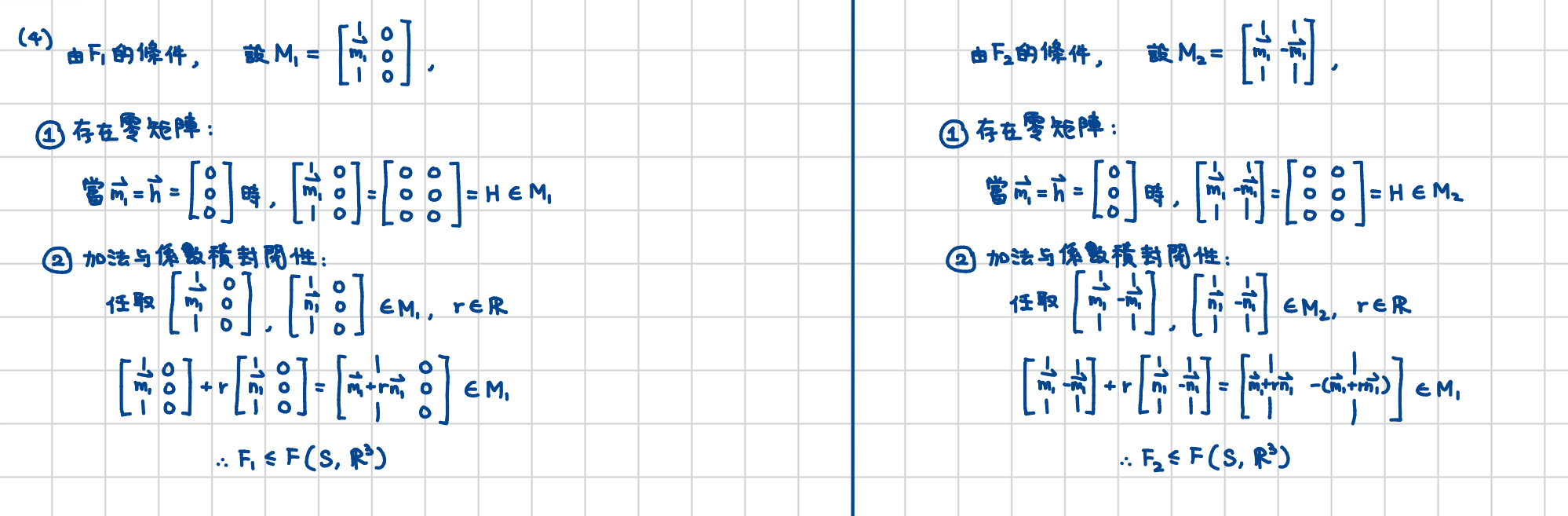


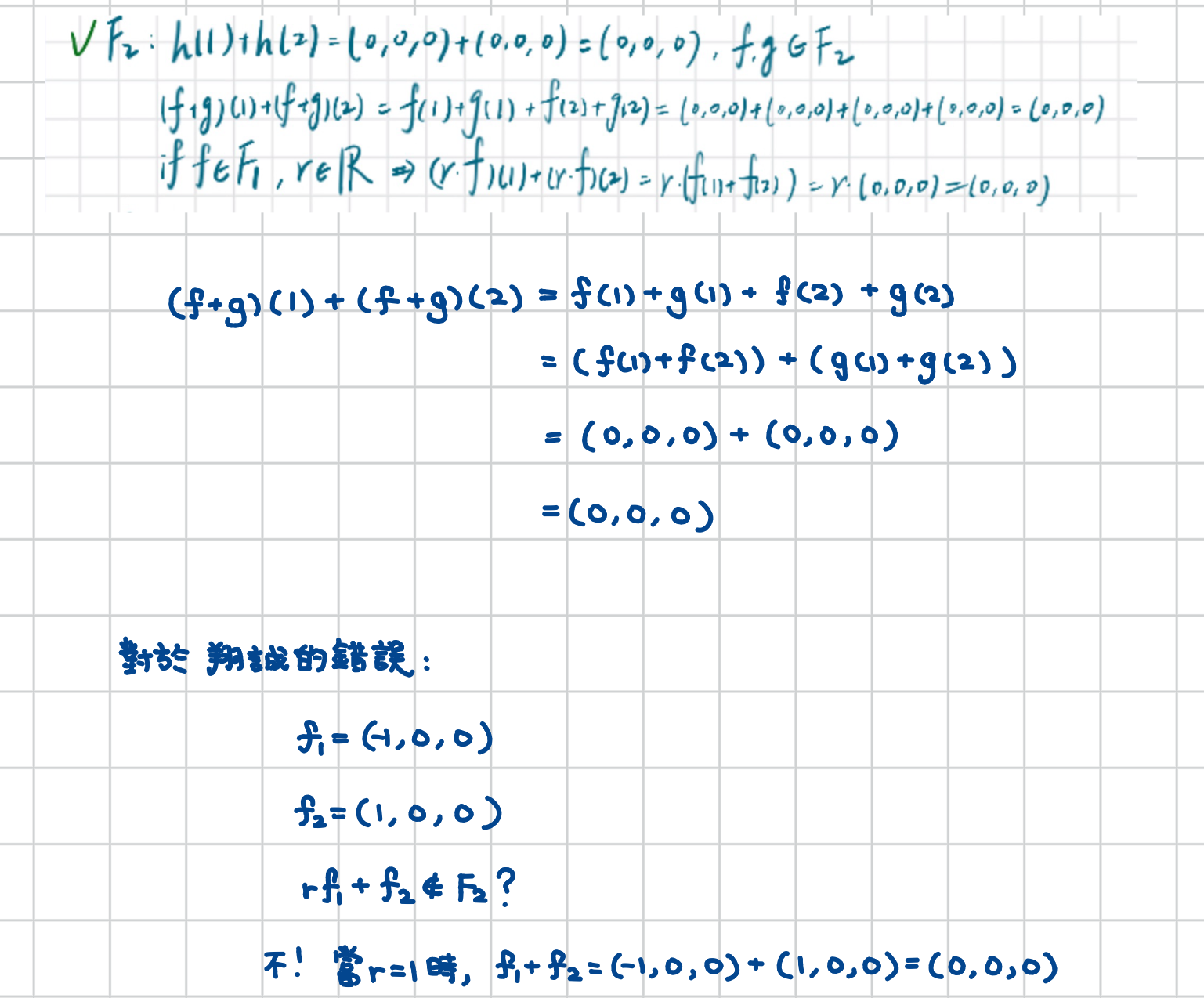
Exercise 3.1